Identificação de Sistema Eletromecânico - Visão Geral¶
Exemplo criado por Wilson Rocha Lacerda Junior
Procurando mais detalhes sobre modelos NARMAX? Para informações completas sobre modelos, métodos e uma ampla variedade de exemplos e benchmarks implementados no SysIdentPy, confira nosso livro: Nonlinear System Identification and Forecasting: Theory and Practice With SysIdentPy
Este livro fornece orientações detalhadas para apoiar seu trabalho com o SysIdentPy.
Mais detalhes sobre estes dados podem ser encontrados no seguinte artigo (em português): https://www.researchgate.net/publication/320418710_Identificacao_de_um_motorgerador_CC_por_meio_de_modelos_polinomiais_autorregressivos_e_redes_neurais_artificiais
import numpy as np
import pandas as pd
from sysidentpy.model_structure_selection import FROLS
from sysidentpy.basis_function import Polynomial
from sysidentpy.parameter_estimation import RecursiveLeastSquares
from sysidentpy.metrics import root_relative_squared_error
from sysidentpy.utils.display_results import results
from sysidentpy.utils.plotting import plot_residues_correlation, plot_results
from sysidentpy.residues.residues_correlation import (
compute_residues_autocorrelation,
compute_cross_correlation,
)
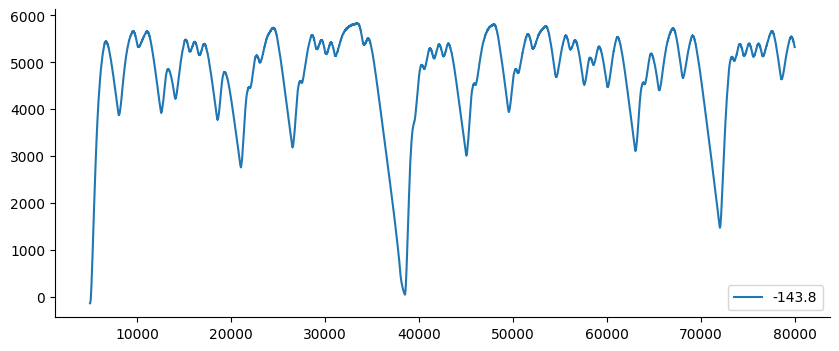
df1 = pd.read_csv("../examples/datasets/x_cc.csv")
df2 = pd.read_csv("../examples/datasets/y_cc.csv")
<Axes: >
# decimaremos os dados usando d=500 neste exemplo
x_train, x_valid = np.split(df1.iloc[::500].values, 2)
y_train, y_valid = np.split(df2.iloc[::500].values, 2)
Construindo um Modelo NARX Polinomial¶
basis_function = Polynomial(degree=2)
estimator = RecursiveLeastSquares()
model = FROLS(
order_selection=True,
n_info_values=100,
ylag=5,
xlag=5,
info_criteria="bic",
estimator=estimator,
basis_function=basis_function,
err_tol=None,
)
model.fit(X=x_train, y=y_train)
yhat = model.predict(X=x_valid, y=y_valid)
rrse = root_relative_squared_error(y_valid, yhat)
print(rrse)
r = pd.DataFrame(
results(
model.final_model,
model.theta,
model.err,
model.n_terms,
err_precision=8,
dtype="sci",
),
columns=["Regressores", "Parâmetros", "ERR"],
)
print(r)
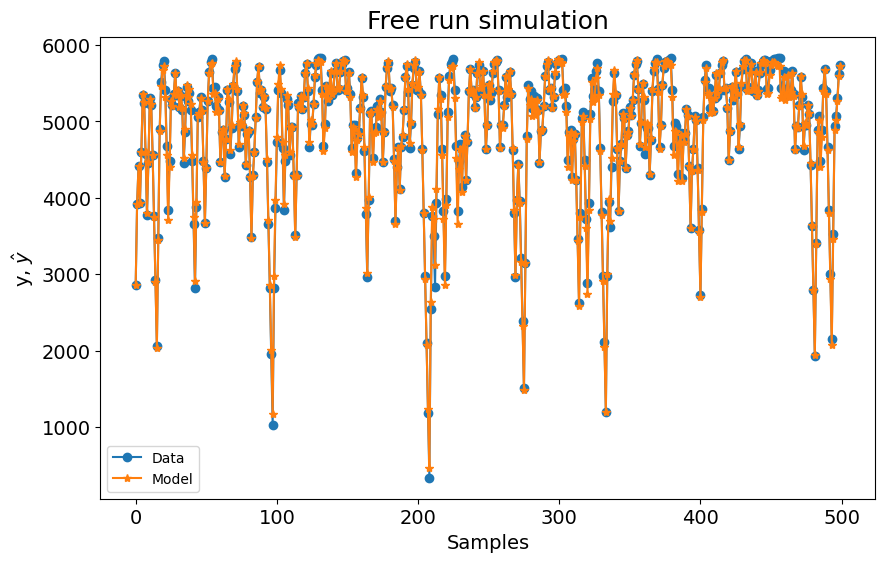
plot_results(y=y_valid, yhat=yhat, n=1000)
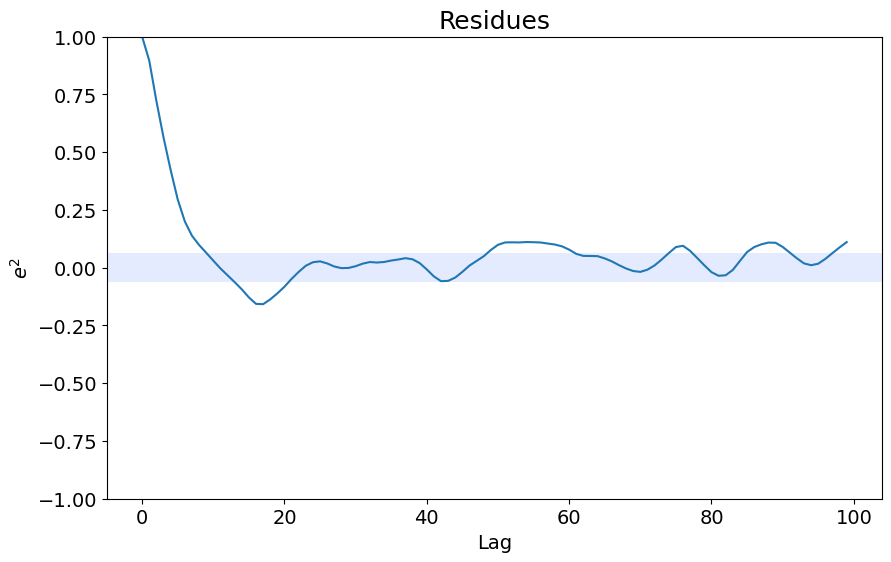
ee = compute_residues_autocorrelation(y_valid, yhat)
plot_residues_correlation(data=ee, title="Resíduos", ylabel="$e^2$")
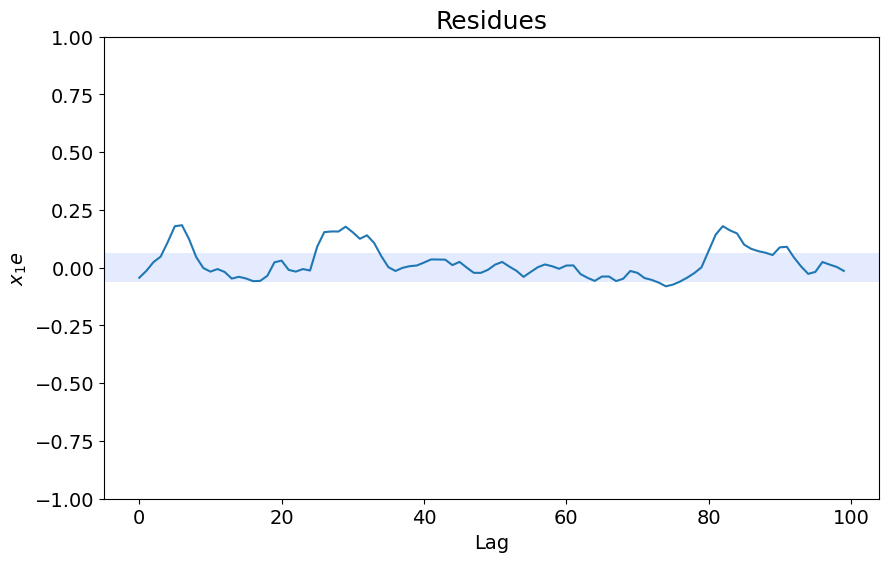
x1e = compute_cross_correlation(y_valid, yhat, x_valid)
plot_residues_correlation(data=x1e, title="Resíduos", ylabel="$x_1e$")
0.05681502501595064
Regressores Parâmetros ERR
0 y(k-1) 1.5935E+00 9.86000310E-01
1 x1(k-1)^2 1.1202E+02 7.94813324E-03
2 y(k-2)^2 -1.7469E-05 2.50921747E-03
3 x1(k-1)y(k-1) -1.5994E-01 1.43297462E-03
4 y(k-2) -7.4013E-01 1.02774988E-03
5 x1(k-1)y(k-2) 1.0771E-01 5.35195948E-04
6 y(k-3)y(k-1) 4.2578E-05 3.46258211E-04
7 x1(k-4)^2 -6.1823E+00 6.91218347E-05
8 x1(k-1)y(k-3) -3.0064E-02 2.83751722E-05
9 y(k-4)y(k-1) -1.4505E-05 2.01620114E-05
10 x1(k-4)x1(k-1) -2.7490E+00 1.09189469E-05
11 y(k-4)y(k-2) 7.2062E-06 1.27131624E-05
12 x1(k-5)y(k-1) -8.5557E-04 6.53111914E-06
13 x1(k-3)x1(k-2) -9.8645E-01 4.24331903E-06
14 x1(k-2)x1(k-1) -2.3609E+00 6.41299982E-06
15 x1(k-3) -2.0121E+02 6.43059002E-06
16 x1(k-1)y(k-5) 3.0338E-03 2.76577885E-06
17 x1(k-3)y(k-1) 3.2426E-02 2.79523223E-06
18 x1(k-4)y(k-1) 5.9510E-03 1.62218750E-06
19 1 -4.2071E+01 1.13359933E-06
Testando Diferentes Modelos Autorregressivos¶
from sklearn.neighbors import KNeighborsRegressor
from sklearn.svm import SVC, LinearSVC, NuSVC
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import (
RandomForestRegressor,
AdaBoostRegressor,
GradientBoostingRegressor,
)
from sklearn.naive_bayes import GaussianNB
from catboost import CatBoostRegressor
from sklearn.linear_model import BayesianRidge, ARDRegression
from sysidentpy.general_estimators import NARX
basis_function = Polynomial(degree=2)
xlag = 5
ylag = 5
estimators = [
(
"KNeighborsRegressor",
NARX(
base_estimator=KNeighborsRegressor(),
xlag=xlag,
ylag=ylag,
basis_function=basis_function,
model_type="NARMAX",
),
),
(
"NARX-DecisionTreeRegressor",
NARX(
base_estimator=DecisionTreeRegressor(),
xlag=xlag,
ylag=ylag,
basis_function=basis_function,
),
),
(
"NARX-RandomForestRegressor",
NARX(
base_estimator=RandomForestRegressor(n_estimators=200),
xlag=xlag,
ylag=ylag,
basis_function=basis_function,
),
),
(
"NARX-Catboost",
NARX(
base_estimator=CatBoostRegressor(
iterations=800, learning_rate=0.1, depth=8
),
xlag=xlag,
ylag=ylag,
basis_function=basis_function,
fit_params={"verbose": False},
),
),
(
"NARX-ARD",
NARX(
base_estimator=ARDRegression(),
xlag=xlag,
ylag=ylag,
basis_function=basis_function,
),
),
(
"FROLS-Polynomial_NARX",
FROLS(
order_selection=True,
n_info_values=50,
ylag=xlag,
xlag=ylag,
info_criteria="bic",
estimator=estimator,
basis_function=basis_function,
err_tol=None,
),
),
]
all_results = {}
for model_name, modelo in estimators:
all_results["%s" % model_name] = []
modelo.fit(X=x_train, y=y_train)
yhat = modelo.predict(X=x_valid, y=y_valid)
result = root_relative_squared_error(
y_valid[modelo.max_lag :], yhat[modelo.max_lag :]
)
all_results["%s" % model_name].append(result)
print(model_name, "%.3f" % np.mean(result))
KNeighborsRegressor 1.168
NARX-DecisionTreeRegressor 0.190
NARX-RandomForestRegressor 0.151
NARX-Catboost 0.121
NARX-ARD 0.083
FROLS-Polynomial_NARX 0.057
for model_name, metric in sorted(
all_results.items(), key=lambda x: np.mean(x[1]), reverse=False
):
print(model_name, np.mean(metric))
FROLS-Polynomial_NARX 0.05729765719062527
NARX-ARD 0.08336072971138789
NARX-Catboost 0.12137085298392238
NARX-RandomForestRegressor 0.15102205613876338
NARX-DecisionTreeRegressor 0.19018792321900427
KNeighborsRegressor 1.1676227184643708